解决方案
SOLUTION

时间: 2024-05-31
浏览量: 4760
Coventor软件的CoventorWare 和MEMS+为RF MEMS的设计、研发、应用提供一个综合平台。
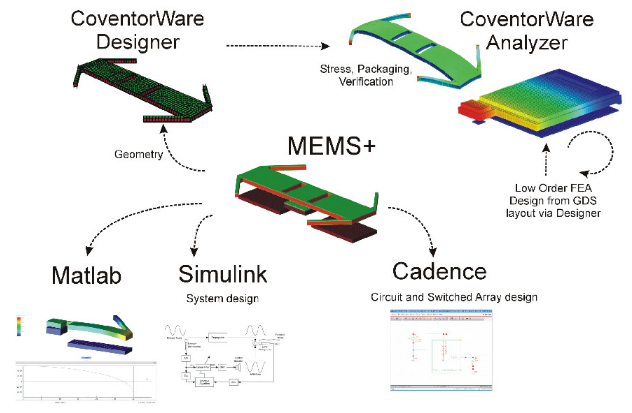
Coventor软件的CoventorWare结合有限元法和边界元法,能精准仿真RF MEMS器件的机械结构、电磁、可靠性和封装等问题,同时MEMS+使用高阶单元,能快速仿真RF MEMS设备的各种多物理场耦合问题,还可以结合MATLAB、Simulink 或者 Cadence进行后续处理和系统级仿真分析。
本文通过选择RF MEMS领域类的一些典型器件,结合Coventor软件模拟,解决RF MEMS设计、研发、应用领域的相关问题。
RF MEMS开关主要有串联和并联两种,按结构分为悬臂梁、膜桥和扭转摆等。接触式串联开关将微波传输线中间断开,通过悬空的微带线的运动实现传输线的通断,常用于DC/6GHz频段。
在RF MEMS开关的分析中,我们主要关注以下这些问题:
本征频率和模态
开关吸合和分离
开启和关断时间
应力应变梯度
在CoventorWare中通过模态分析,我们可以得到RF MEMS开关的本征频率和结构的模态形态,下图为一种RF MEMS开关的前六阶模态效果和本征频率:
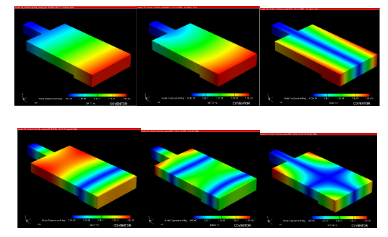
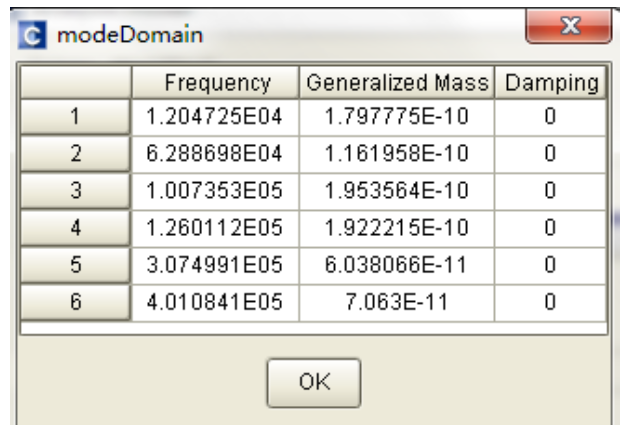
图1 RF MEMS开关的前六阶模态和本征频率
通过CoventorWare Analyzer’s CoSolveEM求解器可以进行RF MEMS开关的 Pullin分析,得到开关的最小吸合电压为13.5V。
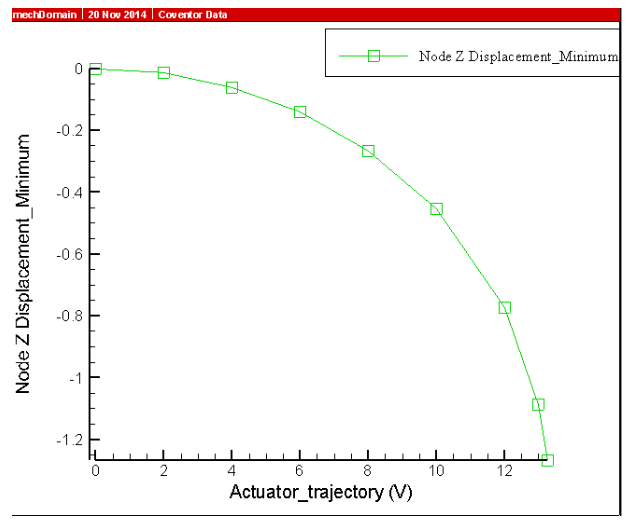
图2 RF MEMS开关悬臂梁Z方向位移与外加电压的关系
进一步的瞬态分析还可以得到,在某一电压条件下,开关的关断时间:
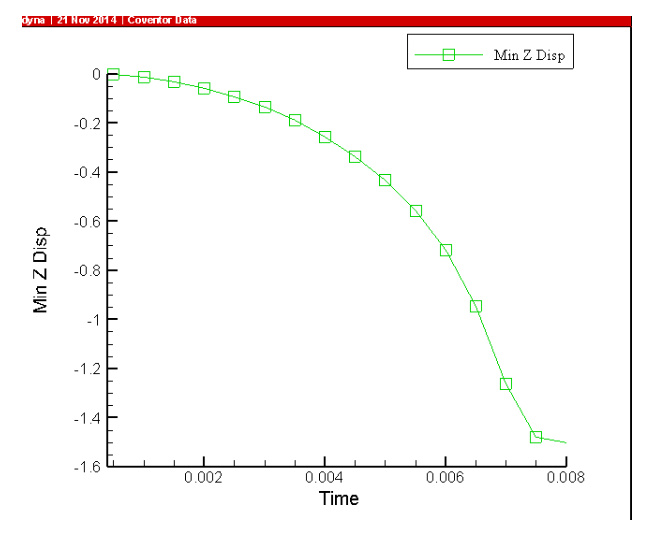
图3 开关位移随时间变化关系
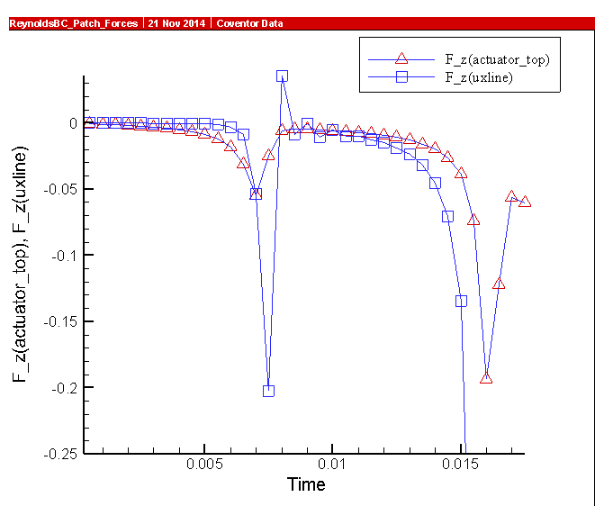
图.4 考虑流体阻尼时的开关位移与时间的变化关系
本模型的难点在于吸合分析时机械接触的高度非线性,同时开关在闭合和开启时,空气层的变化使得基于体积的传统有限元工具很难模拟出真实的结果,这些软件往往需要随着开关的移动不断重新剖分网格,使得瞬态的计算难以进行。下图是两个不同时间节点的压力分布结果:
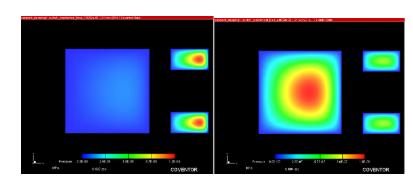
图5开关执行器和接触板上的压力分布
Film Bulk Acoustic Resonator (FBAR)由薄膜压电层覆盖一个在衬底上刻蚀的空气腔构成。经过器件的RF信号在压电层产生机械长度上的振动。当膜层厚度是信号半波长的整数倍时,谐振条件满足,我们就可以观测到谐振现象。在谐振时,电阻抗有一个锐利的变化,实现了频率选择滤波器的设计。设计者通常争取实现最大Q值频率附件的最小非物理模。
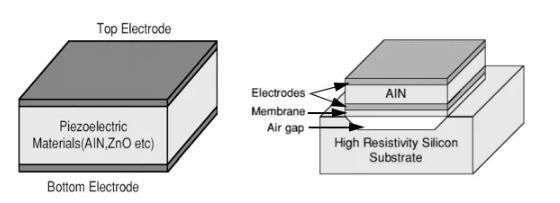
图6 FBAR设备构成图
使用CoventorWare软件,我们可以仿真压电谐振器在开环和闭环条件下的工作特点,如下图7是通过DC响应分析,得到FBAR的mises应力分布、电势和位移分布图:
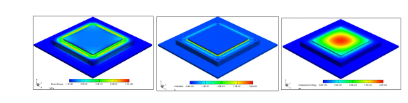
图7 压电谐振器mises应力、电势及位移分布图
压电谐振器闭环模态分析,以此来预测谐振器的串联谐振频率,外接零电势边界条件时,压电部分的顶面和底面沿着长度方向反向运动时,呼吸模式出现。通过仿真分析,得到基模频率为1.95GHz,基模和高阶模式结果见下图:
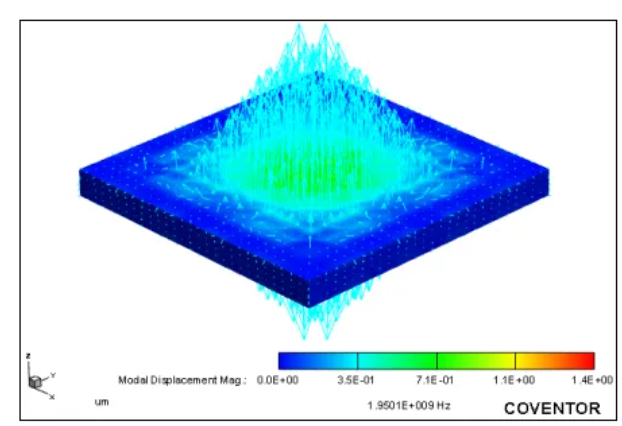
图8 闭环响应中的呼吸模式
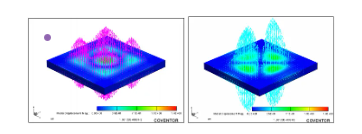
图9 闭环响应中的高阶长度形变模式
分析压电谐振器开环模态,可以预测谐振器的并联谐振频率,仿真结果如下,根据基模的振动频率可以得到谐振器的并联谐振频率约为2.02 GHz。
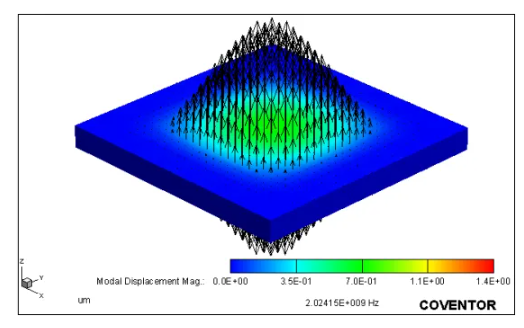
图10 开环响应中的基本呼吸模式
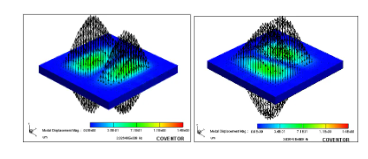
图11 开环响应中的高阶退化呼吸模式
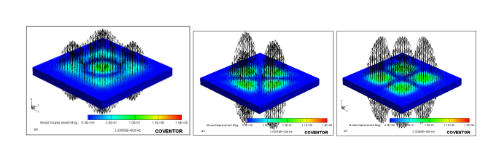
图12 开环响应中的高阶呼吸模式
通过谐振器电阻抗的幅值和相位分析,可以得到谐振器的谐振点、非物理模和反谐振点:
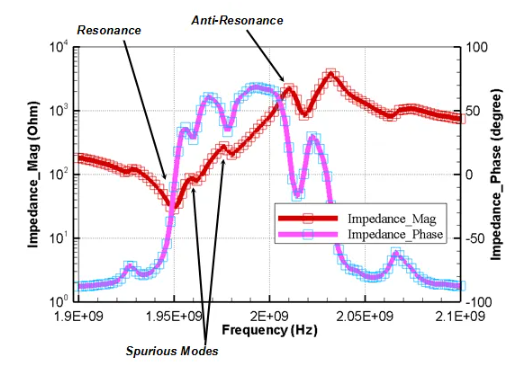
图13 FBAR频率响应分析
下图显示一个高Q值高频MEMS滤波器,在仿真分析时,关心以下这些性能:
带宽和阻带抑制
中心频率的静电调谐
功率容量和动力非线性
热稳定性
损耗机制
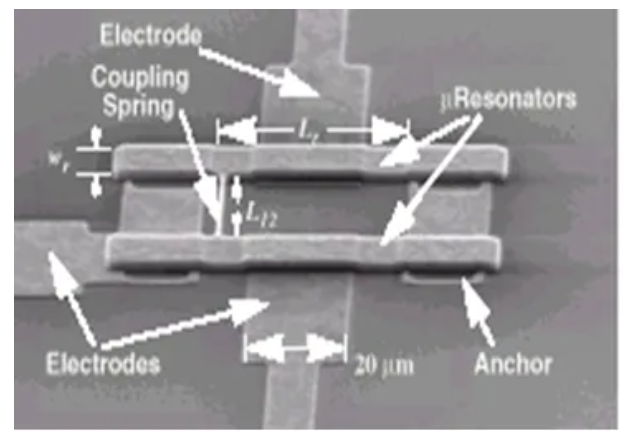
图14 高Q值高频MEMS滤波器
通过Coventor MEMS+软件的建模仿真,可以得到该滤波器的频率响应如下:
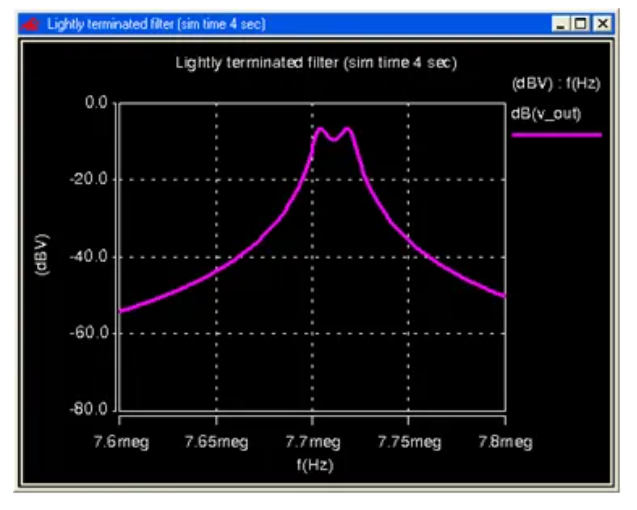
图15 高Q值高频微机电滤波器频率响应曲线
对于不同的梁的长度下频率响应进一步的仿真分析,得到曲线如下图16,可以看出随着梁长度的增加,滤波器的带宽变窄。
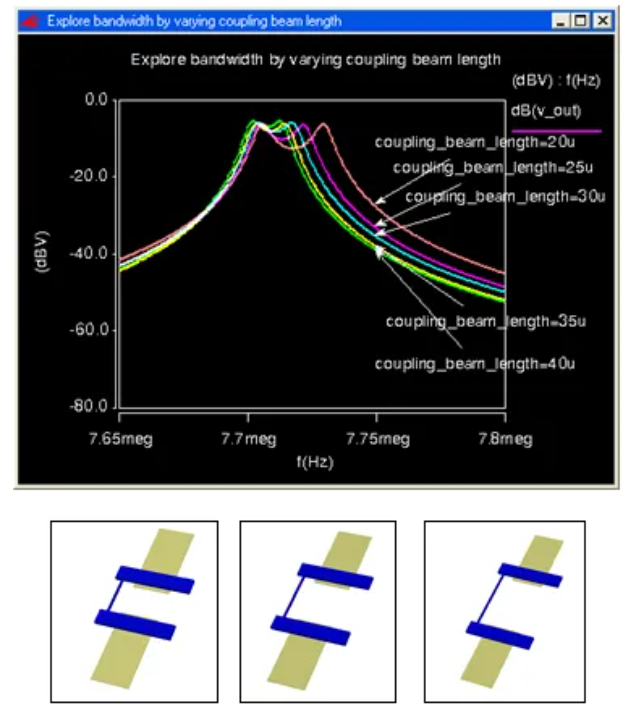
图16 不同梁长度下的频率响应曲线
滤波器使用直流偏压来调整中心频率,仿真结果如下:
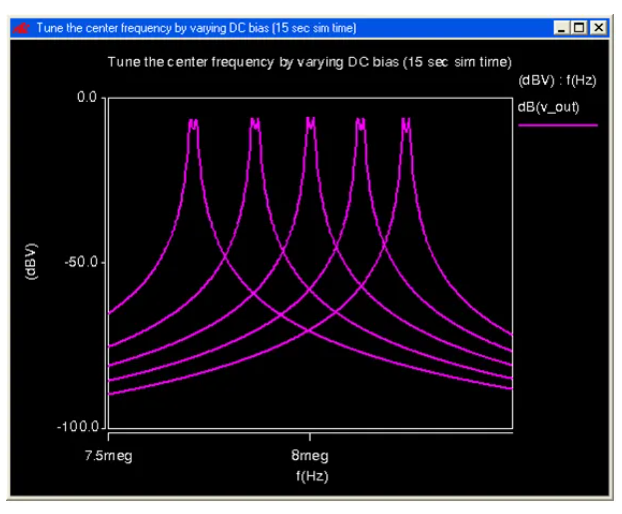
图17通过改变直流偏压调节滤波器中心频率
MEMS谐振器中的非线性会导致交越失真、幅值和功率容量的受限、影起参考时钟的相位噪声。下图18中相位图显示了不连续性。
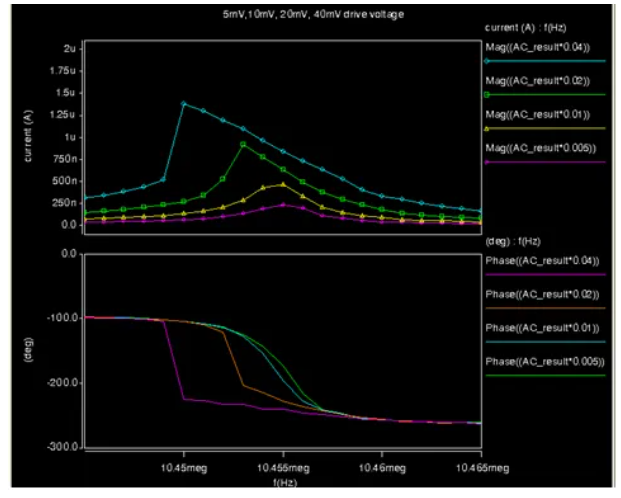
图18 7V直流偏压下的非线性分析
对于MEMS设计者所关心的将滤波器模型耦合到电路中,实现系统级分析的问题,MEMS+提供了与MATLAB Simulink和Cadence Virtuoso软件的接口,方便在Simulink或者Cadence中调用模型做后续的分析,如下图,显示了将本例中的MEMS谐振器作为元器件来构成振荡器。
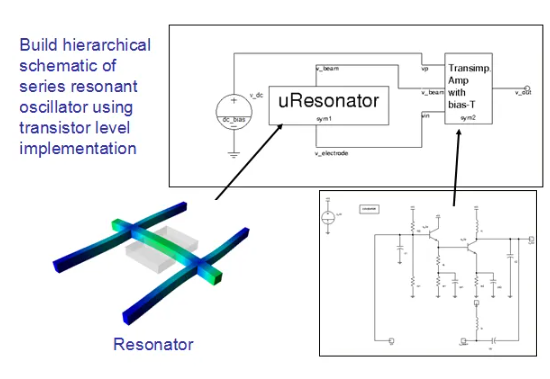
图19 从谐振器来构建振荡器的实现
阻尼分析中通常使用以下公式来计算不同类型损耗对于器件Q值的影响:
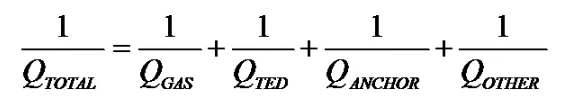
图20显示了了谐振器的SEM图像和使用Coventor软件仿真得到的一阶模态效果,
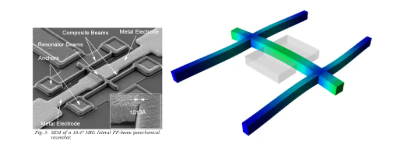
图20 谐振器的SEM图像及一阶模态效果图
通过Coventor软件仿真,还计算可以得到谐振器的热弹性损耗、气体阻尼损耗和锚点损耗等,部分结果如下图:
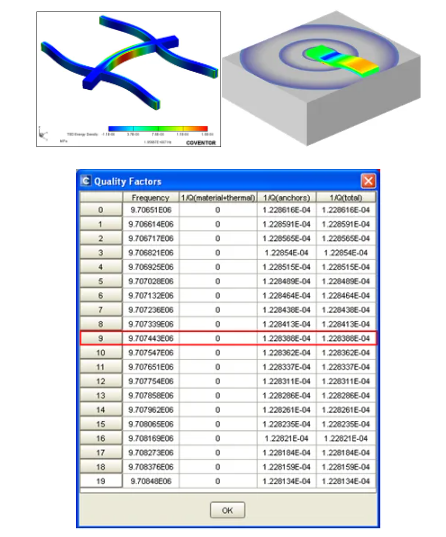
图21 谐振器的热弹性损耗下的模式及锚点损耗Q值
MEMS产品实现商品化的前提必须解决封装问题,因为MEMS产品容易受周围环境的影响,RF MEMS电路正常工作很大程度上取决于由封装所提供的内部环境与保护。下面的案例显示了在温度上升了情况下MEMS设备封装的变形:
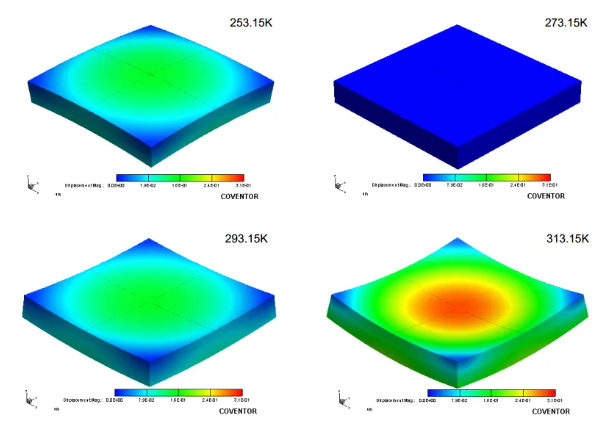
图22 封装变形与温度的变化关系
下图显示了封装温度和位移上升的情况下梳齿的分离:
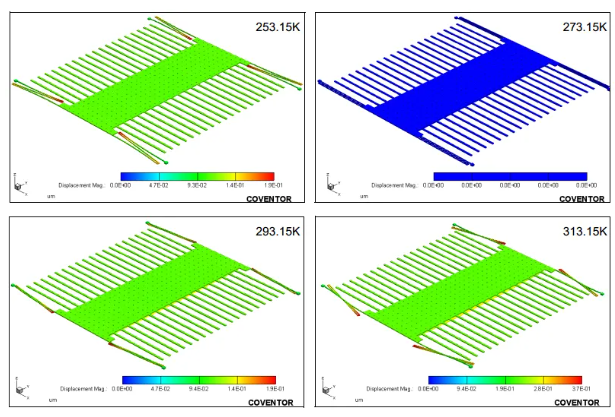
图23 封装温度和位移增加时梳齿逐渐分离
MEMS谐振器具有极高的Q值,很低的损耗,很宽的工作频率范围以及灵活的结构设计和材料选择等特点,在谐振器设计过程中,主要关注以下问题:
找到满足目标频率谐振的几何
阻抗匹配
可靠性:应力消除
封装效应
频率稳定性
减小相位噪声,包含降低损耗和功率容量的分析
下图显示了使用MEMS+设计的不同几何形状的谐振器及仿真分析得到的谐振频率。
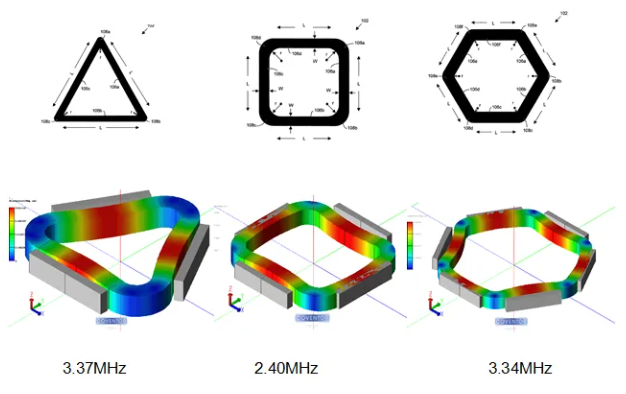
图24 不同谐振器设计及其谐振频率与模态
使用MEMS+ with MATLAB扫描连梁长度来计算模态频率,优化设计谐振器阵列排布:
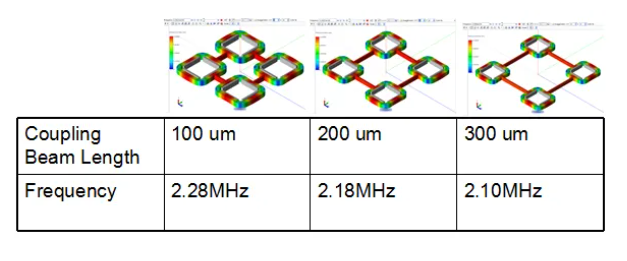
图25不同连梁长度的谐振器阵列模态频率
锚点设计,减小锚点应力,降低锚点损耗,
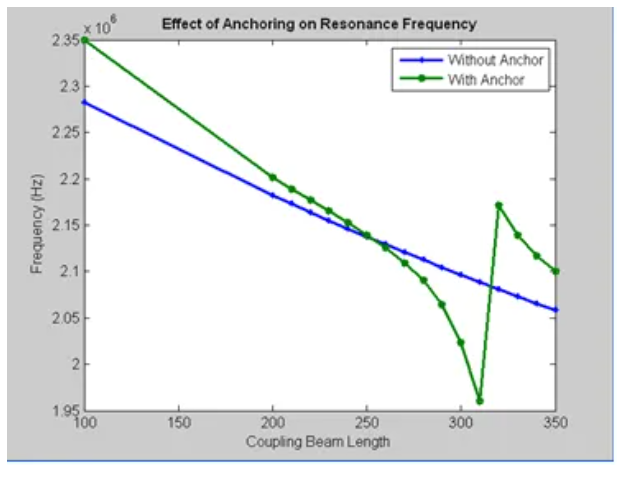
图26 在有锚点和无锚点条件下谐振频率与连梁长度的关系
从上图可以看出,选择250um的梁长度可以最小化锚点的影响。
频率稳定性分析结果如下:
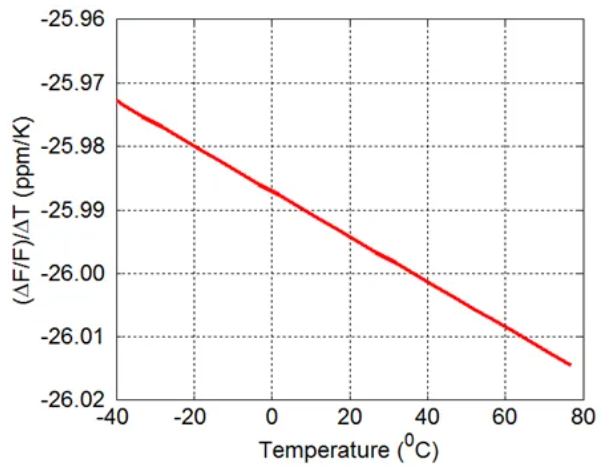
图27 温度影响下的频率稳定性关系
使用MEMS+可以自动将MEMS谐振器的电路集总参数提取出来,并且实时在Cadence Virtuoso 和Mathworks Simulink and MATLAB调用,通过与这些系统级软件联合仿真,展示模型对于输入电激励的输出响应,下图显示了MEMS谐振器的电路响应、模型与温度和直流偏压的关系:
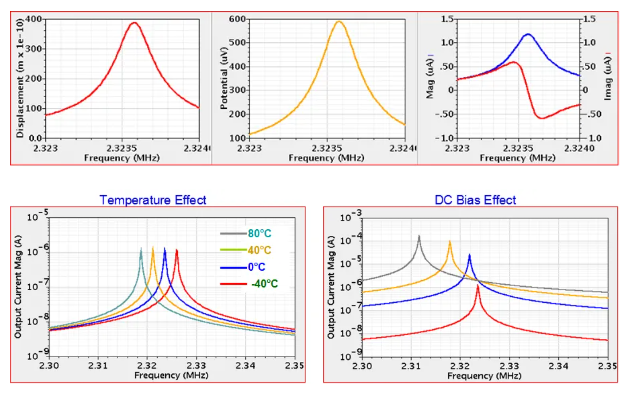
图28 模型电路响应及与温度和直流偏压的关系
上图显示了在MEMS谐振器的输出位移、输出感应电压、输出感应电流以及与温度和直流偏压的关系。
应力释放的优化设计,使用0.18um的圆角和20um的圆角时,谐振器梁角的应力分布可以通过Coventor模拟,减小应力过度集中的情况。
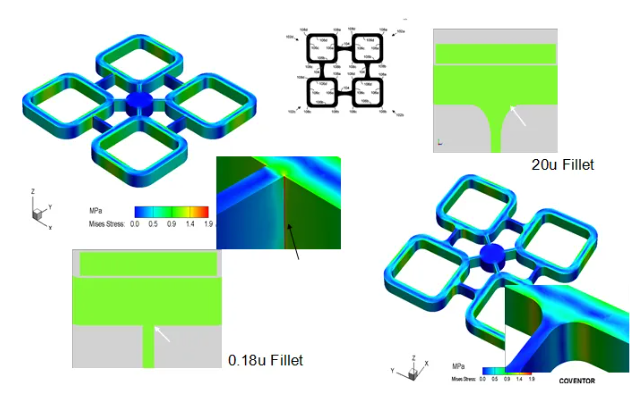
图29应力释放的仿真分析结果
同样,使用软件可以仿真计算谐振器的锚点损耗,仿真效果如下:
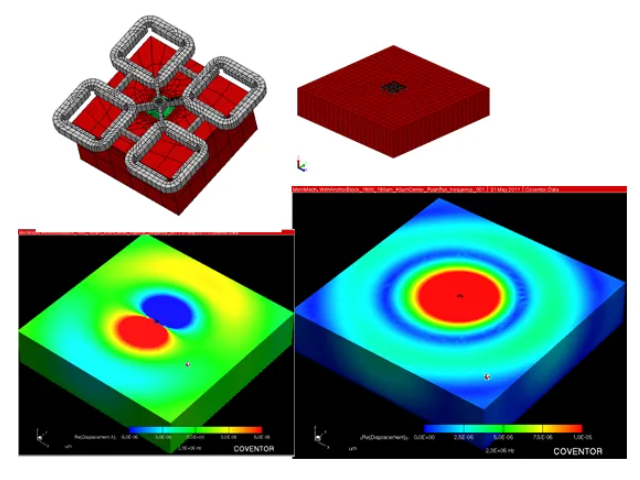
图30 锚点损耗的仿真分析结果